type
status
date
slug
summary
tags
category
icon
password
Last edited time
Apr 14, 2023 09:15 AM
课程介绍
课程安排

Java环境搭建
这里我就略了。我是用idle。下次补充。下次一定。
题解
参考。
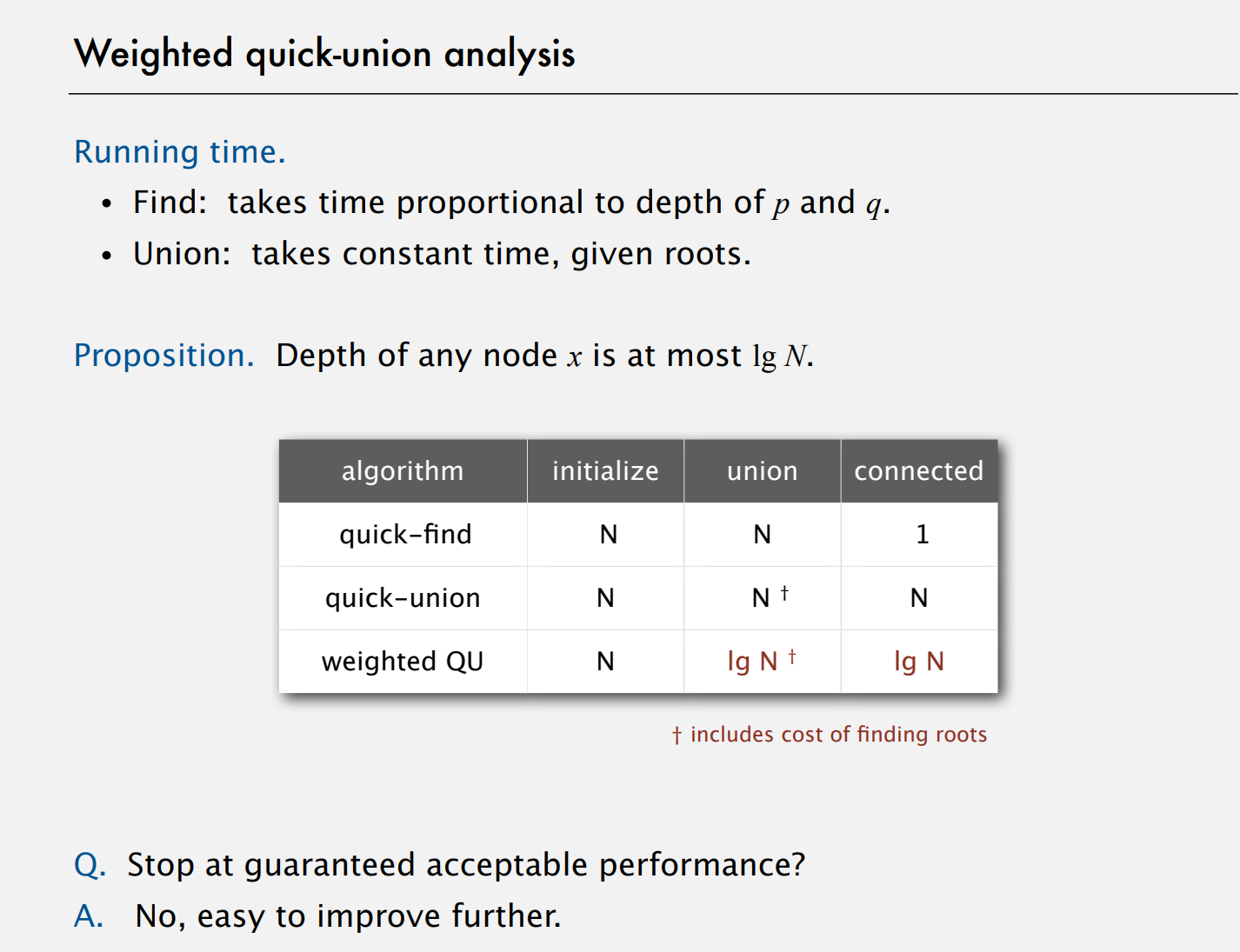
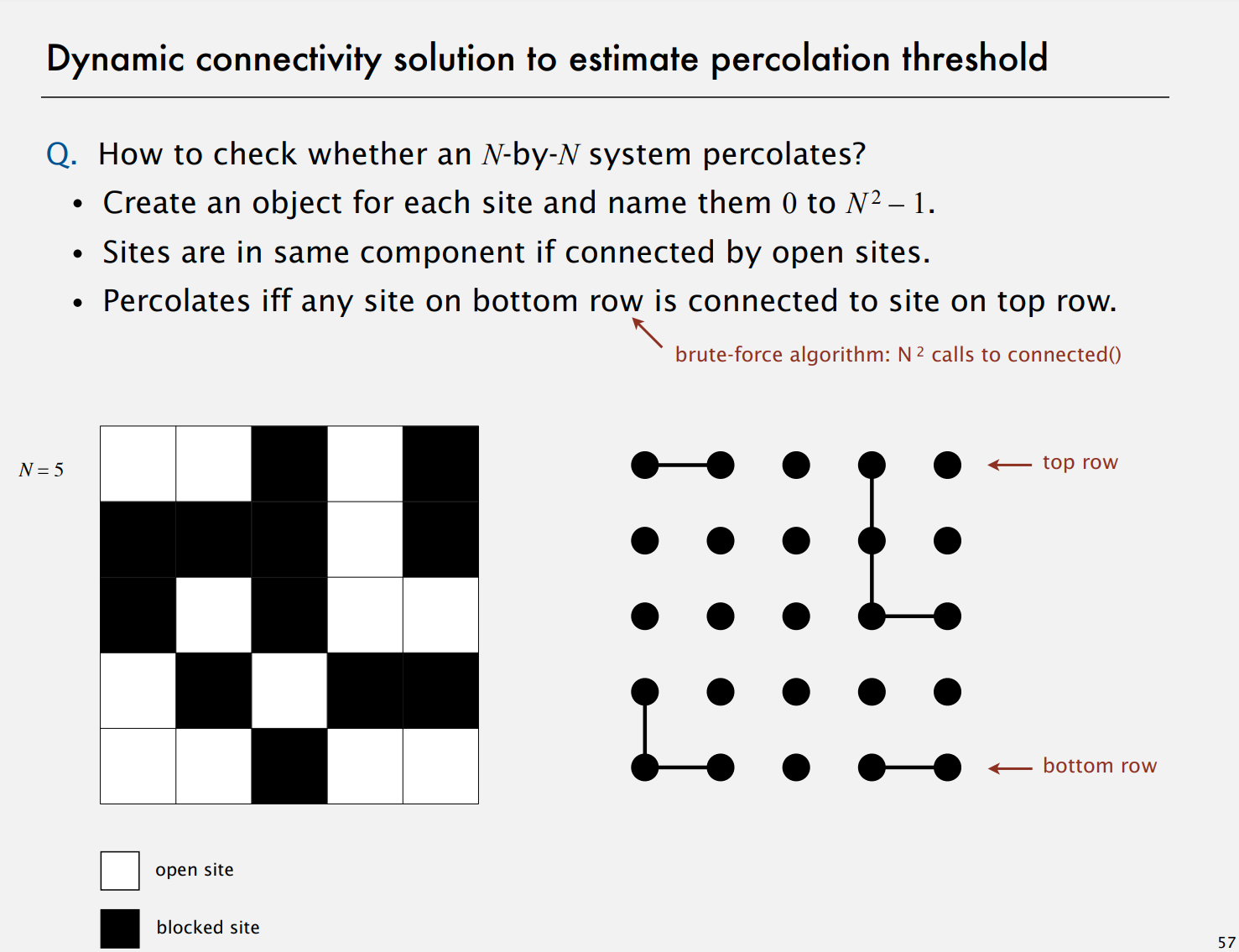
案例研究:Union-Find算法
图的动态连接性问题
输入是一系列整数对,其中每个整数代表某种类型的对象,我们将
p q 对解释为表示 p 连接到 q 。我们假设“被连接到”是一个等价关系。等价关系将对象划分为等价类或连通分量。我们的目标是编写一个程序来从序列中过滤掉无关的对:当程序从输入中读取一对
p q 时,只有当它看到的对不暗示时,它才应该将该对写入输出 p 连接到 q 。如果前面的对确实暗示 p 连接到 q ,那么程序应该忽略对 p q 并继续读取下一对。因此我们需要创建一个叫UF的类,它包含两个方法,一个用来实现合并,另一个用来实现连接查找,返回一个布尔量(逻辑变量,真或者假)。构建器需要对象的数量作为参数这样它能够根据对象的数量建立数据结构,那么当我们在实现算法的时候,我们要在心里牢记对象的数量和操作的数量都可能是巨大的,我们可能会有非常大量的合并与连接查询操作,而 我们的算法在这样的情况下也必须是高效的。
检查我们的应用编程接口(API)设计,我们通过设计一个使用我们开发的数据类型的客户端来检查API。比如这个例子中我们已经有了一个客户端从标准输入中读取信息。首先读取一个整数,表示将要处理的对象的数量。然后是一对一对对象名字,客户端首先从标准输入中读取这个整数并创建一个UF对象。然后只要标准输入中还有输入客户端将从输入读取两个整数。如果它们没有相连,它将会连接他们并输出。如果它们已经相连,客户端就忽略这条输入。
以下 API 封装了我们需要的基本操作。

https://algs4.cs.princeton.edu/15uf/UF.java.html
这个网址中的java代码中的
main() 解决了动态连接问题。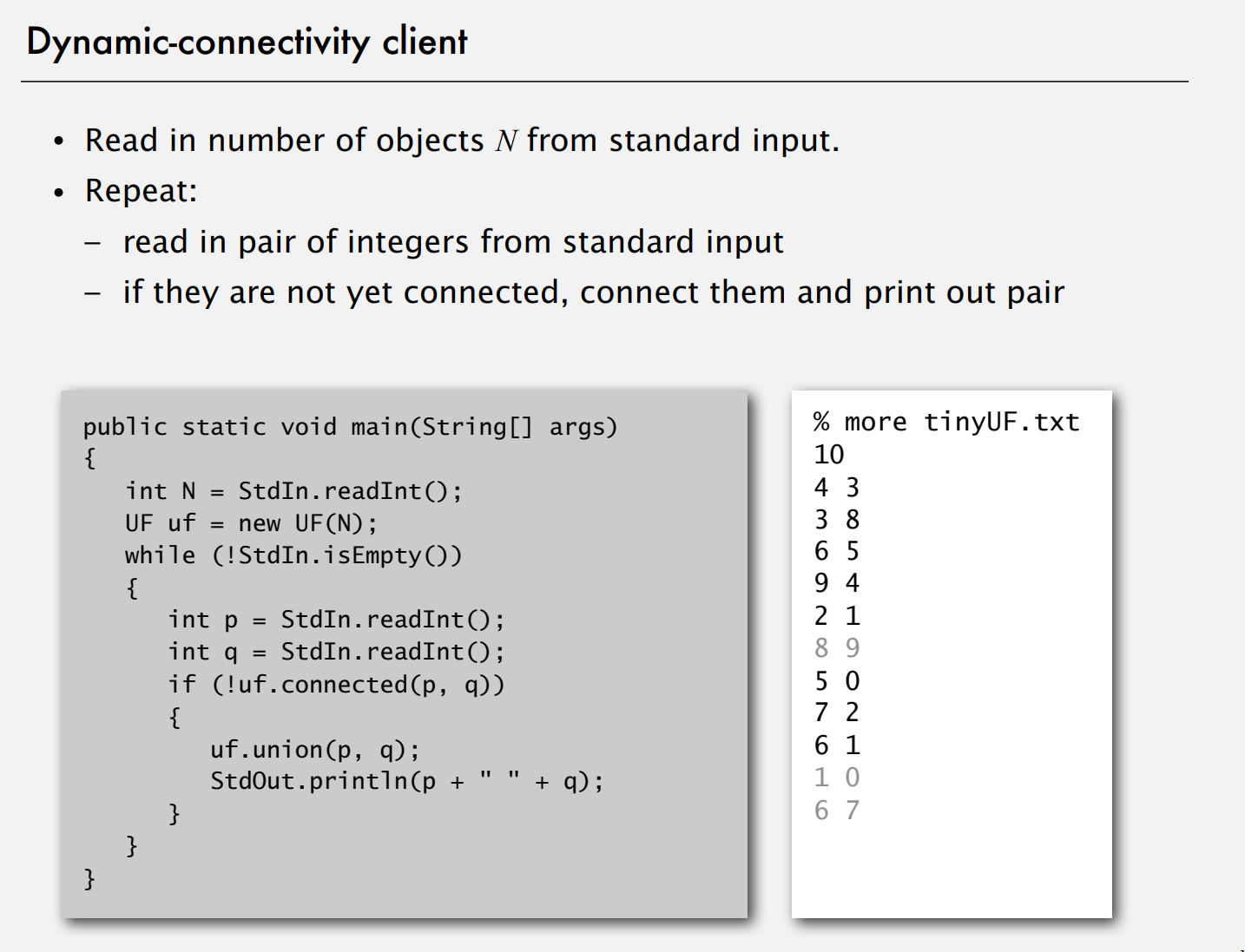
Quick-Find算法
我们现在考虑几种不同的实现,所有实现都基于使用站点索引数组
id[] 来确定两个站点是否在同一组件中。首先是Quick-Find算法。它的实现在https://algs4.cs.princeton.edu/15uf/QuickFindUF.java.html中。快速查找算法的基本思想是这样的,用id[]来表示p和q当前所在的组,即当且仅当
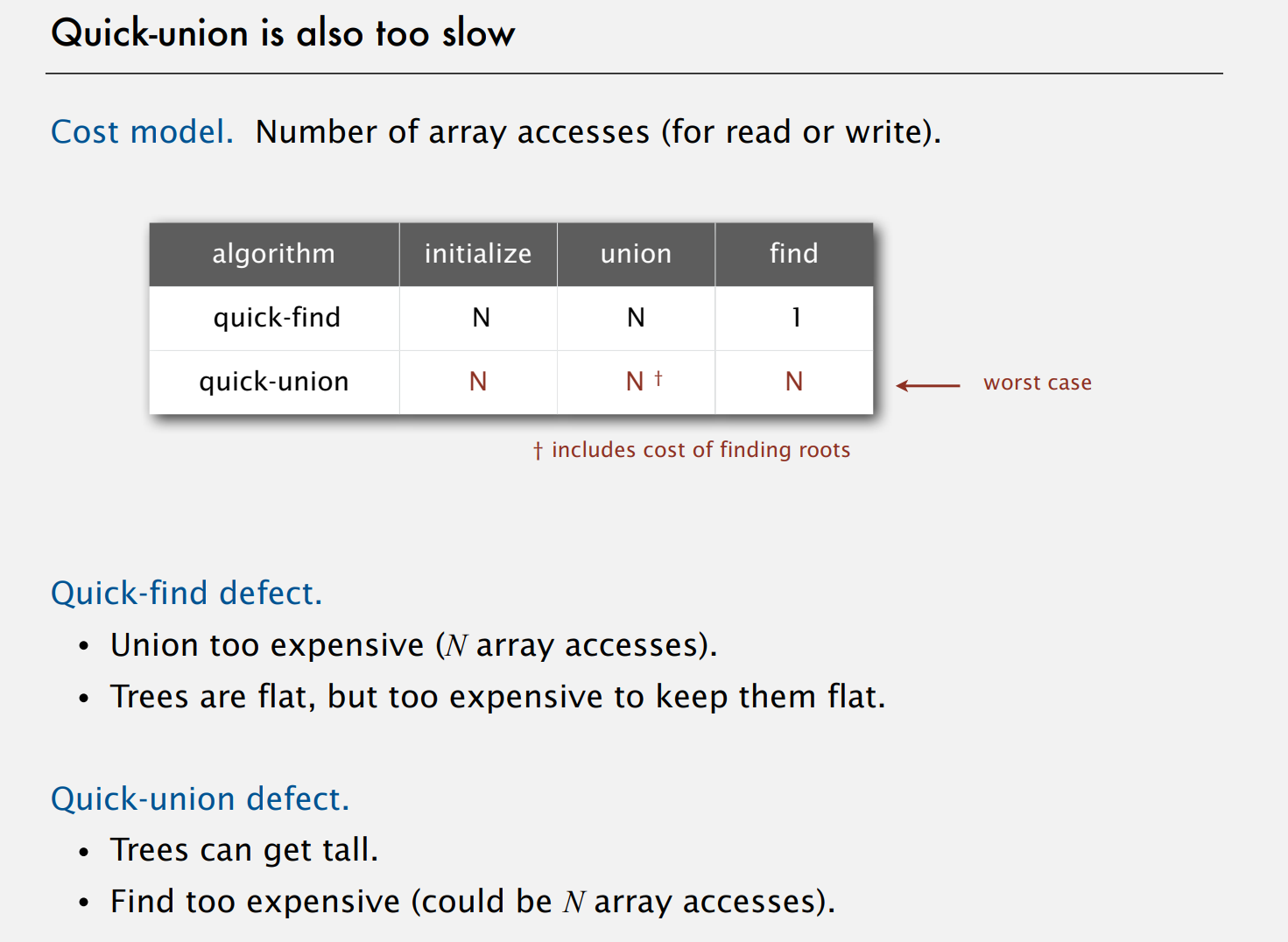
id[p] 等于 id[q] 时, p 和 q 才相连。这样子为了找p所在的组就会很快,直接调用id[p]就可以,但是合并操作会慢许多,因为要变换所有id[p]位id[q]。
这是一些改动:


Quick-Union算法
快速合并算法。 QuickUnionUF.java 基于相同的数据结构——站点索引的
id[] 数组——但它使用不同的值解释,从而导致更复杂的结构。具体来说,每个站点的 id[] 条目将是同一组件中另一个站点的名称(可能是它本身)。也就是id[i]表示i的parent。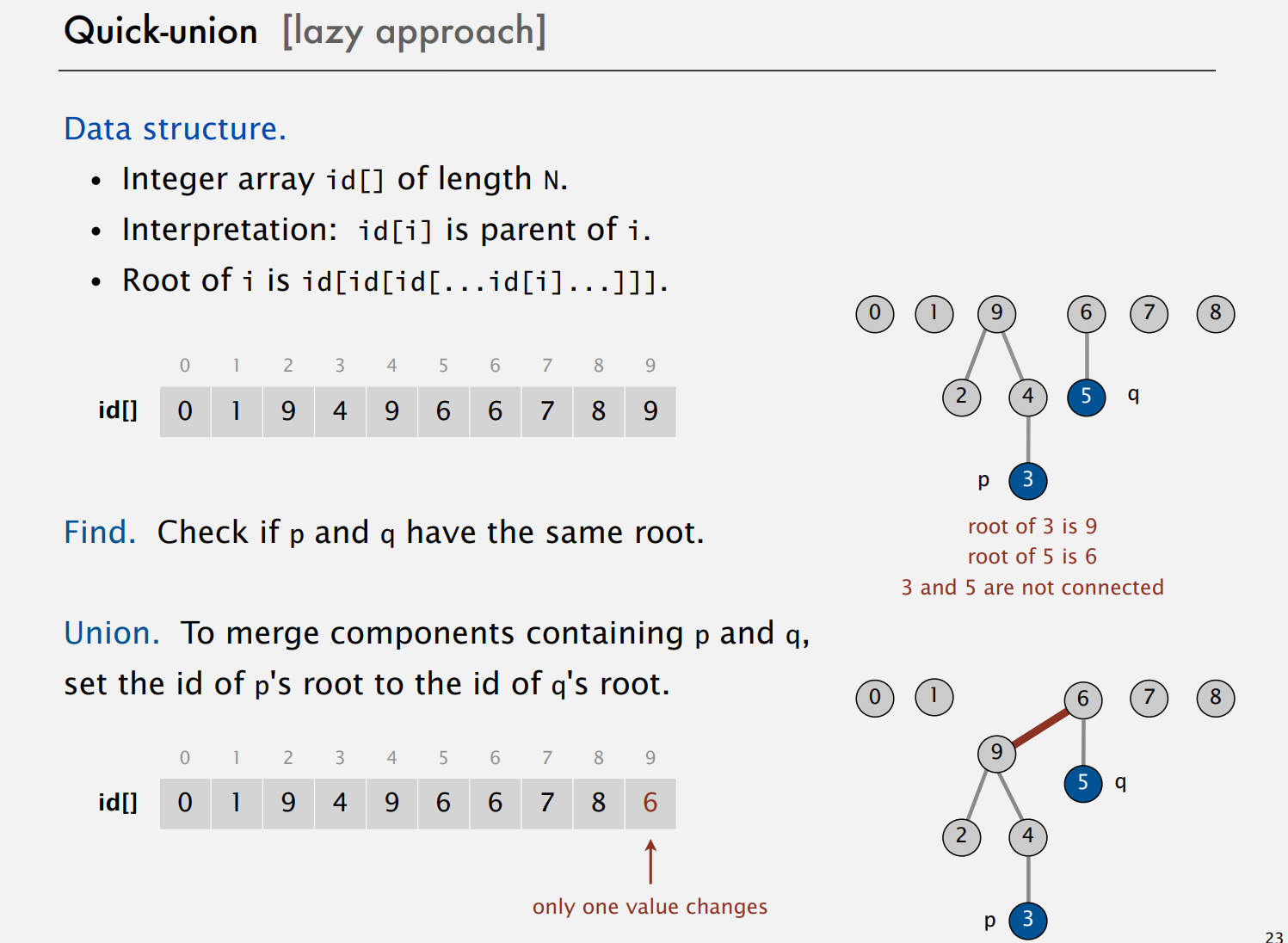
下面是它的代码变化:
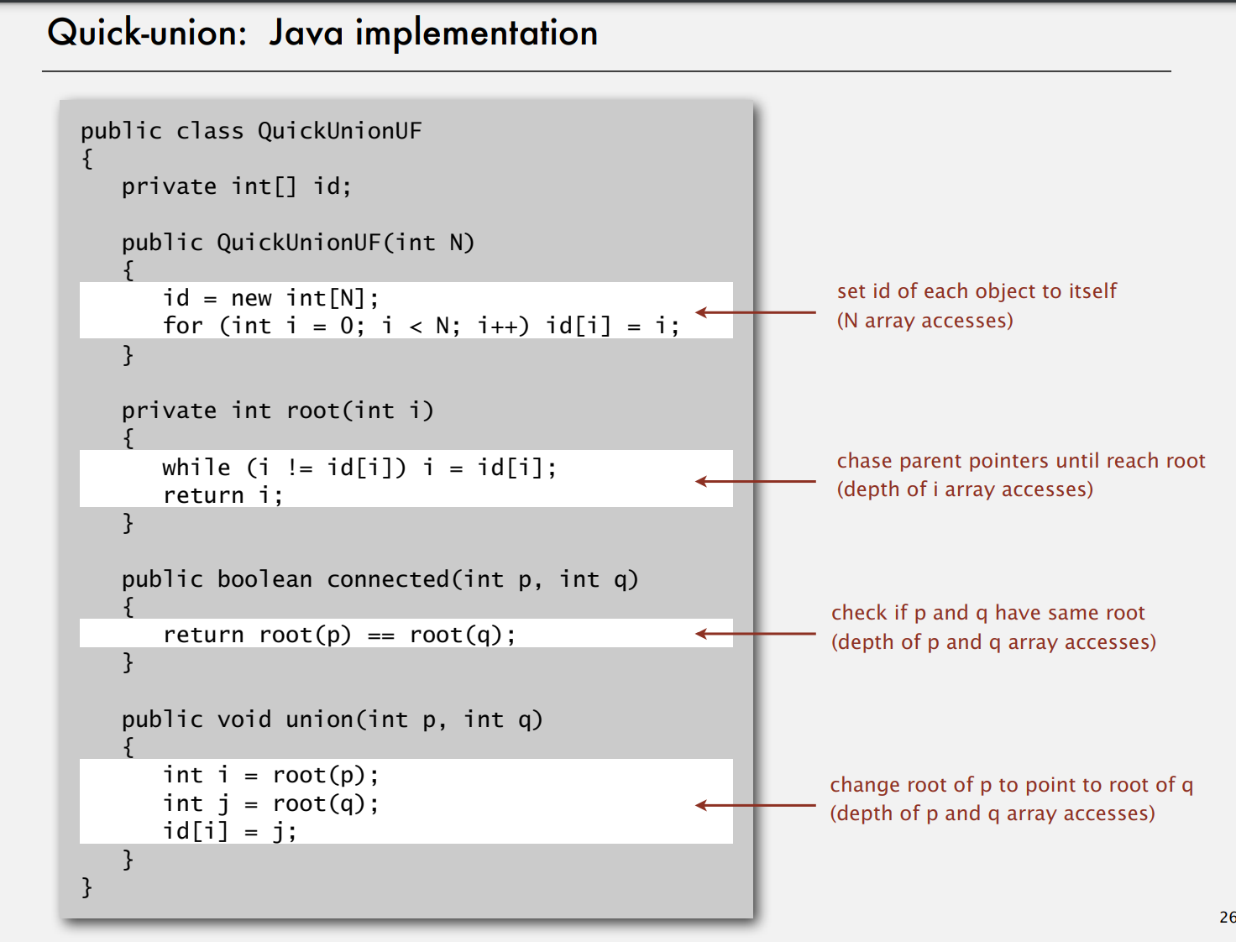
两种算法的对比与优缺点分析:
Weighted-Union算法
加权快速联合。对于快速联合算法中的
union() ,我们不是任意将第二棵树连接到第一棵树,而是跟踪每棵树的大小,并始终将较小的树连接到较大的树。程序 WeightedQuickUnionUF.java 实现了这种方法。代码的变化:

这样可以让树不过于太深,更加扁平化。 可以证明树的深度至多是lgN

对比:
带路径压缩的Weighted-Union算法
带路径压缩的加权快速联合。有许多简单的方法可以进一步改进加权快速联合算法。理想情况下,我们希望每个节点都直接链接到其树的根,但我们不想付出改变大量链接的代价。我们可以通过使我们检查的所有节点直接链接到根来简单地接近理想。

当我们试图寻找包含给定节点的树的根节点时,我们需要访问从该节点到根节点路径上的每个节点。与此同时我们可以将每个节点都指向根节点。所以当我们找到P的根节点之后,可以回过头来将路径上每个节点都指向根节点,这需要常数的额外代价,我们回溯一次路径找到根节点,然后再回溯一次将树展平。令人惊奇的是,我们只需要添加一行代码就能将树展平。实际上,为了只添加一行代码,我们稍做了一点改变:我们将路径上每个节点指向它在路径上的祖父节点。
lg* N是个挺有意思的函数。它是使N变为1需要取对数的次数,它叫做迭代对数函数。在真实世界中可以认为是一个小于5的数,因为lg*(2^65536)=5
x | lg* x |
(−∞, 1] | 0 |
(1, 2] | 1 |
(2, 4] | 2 |
(4, 16] | 3 |
(16, 65536] | 4 |
(65536, 2^65536]2 | 5 |
就是$2^1,2^{2},2^{2^{2}},2^{2^{2^{2}}}$
Hopcroft Ulman和Tarjan证明了如果有N个对象,M个合并与查找操作的任意序列,需要访问数组最多c(N + M lg* N)次。这说明带路径压缩的带权快速合并算法在真实世界中的时间复杂度是线性的,而实际上可以改进到
一个更有意思的函数,Ackermann函数,这个函数增长速度比 lg* 还慢 另外一点要说明的是看起来这个算法的时间复杂度已经非常接近与N成正比的线性了.它与N乘一个关于N的增长非常缓慢的函数成正比。那么是否存在一个简单的算法其时间复杂度就是线性的呢?人们找了很久,实际上最后证明了这样的算法是不存在的。

下面是总结:

一些应用
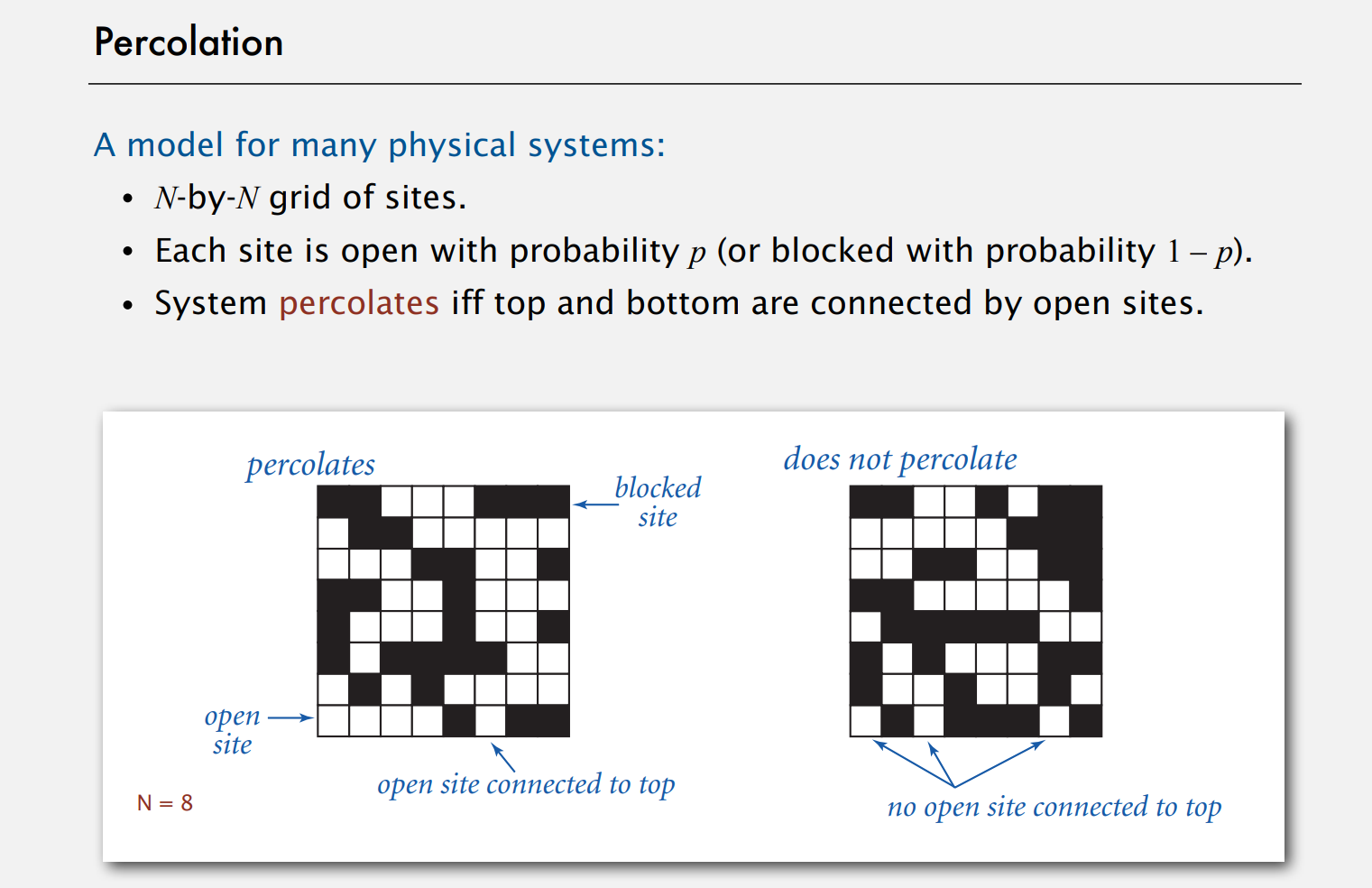
在底层应用中其中一个很重要的是在图像处理中如何标记图像中的区域。后续的课程中我们会看到Kruskal最小生成树算法,这是一个使用并查集作为子程序的图处理算法。我们接下来会看一个例子是物理中用来理解物理现象的一个算法。这个列表里还有很多其他例子好,我们现在要讲的这个叫渗滤(percolation)。这是很多物理系统的模型。
我们考虑一个n×n的方形网格,小方格叫做位。每个位是开放的概率为p如图中为白色方格。位是闭合的概率为1-p,如图中为黑色方格。我们定义一个系统是渗滤的如果顶端和底端被开放的位连通。所以左边的系统中可以找到一条通过白色方格从上到下的路径而右边的系统不是渗滤的。不存在通过白色方格从上到下的路径。这是很多系统的模型,你可以认为它是电力系统,可以认为开放的位是导体,闭合的位是绝缘体。所以如果存在从上到下的导体那么系统就是导电的。或者可以认为水流过某种多孔的物质,开放位就是空的,闭合位有一些材料,是否渗滤就是水能否从上端流到下端。或者可以认为这个系统是社交网络人们互相有联系,两个人之间可能有,也可能没有联系。
当概率p很小 系统不渗滤。当概率p很大,系统就是渗滤的。实际上系统是否渗滤的概率p阈值非常陡峭,而且存在一个值,当N非常大时p小于该值时,系统基本肯定不是渗滤的,如果大于该值基本一定会渗滤。问题就是那个值是多少。这是一个问题被数学模型精确描述的例子。没有人知道那个数学问题的解,我们有的唯一的解来自计算模型。
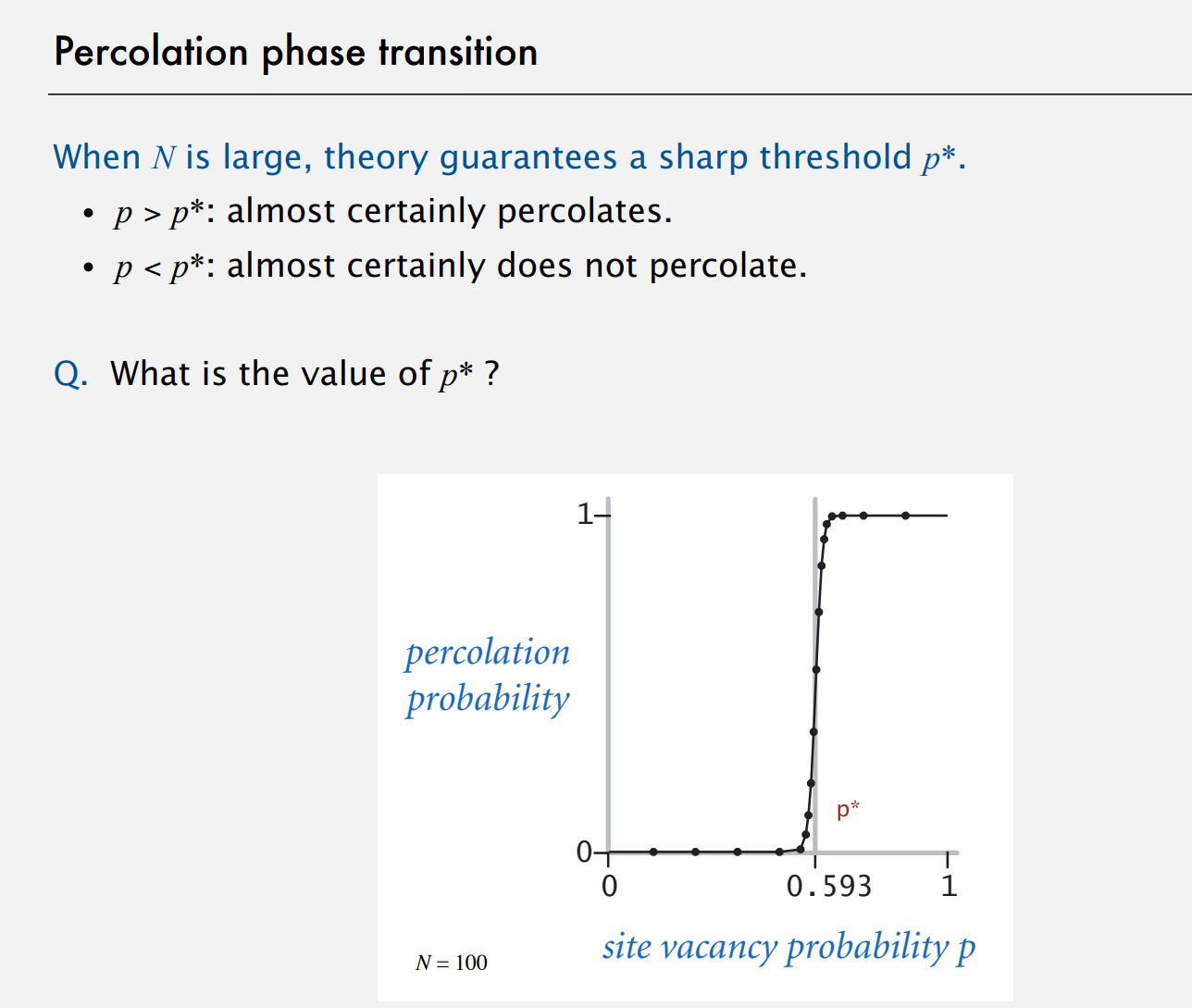
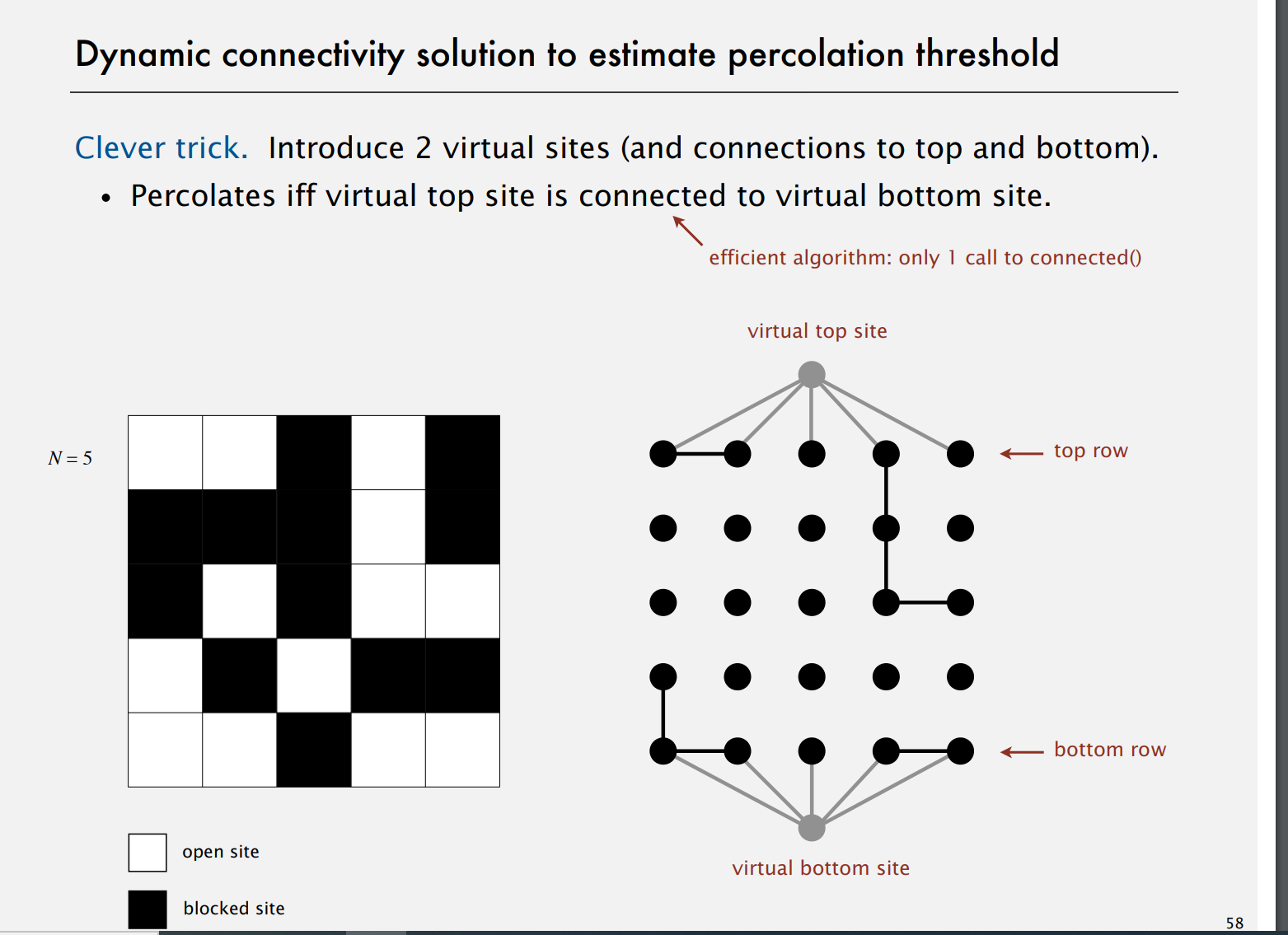
为了解决这个临界值的问题,我们进行蒙特卡洛模拟。
想知道系统是否渗滤时,只需要检查虚拟顶端位和虚拟底端位是否连通。那么我们要怎么对开放新位建模呢?开放一个位我们只需要将它和它周围的开放位连通。所以需要调用几次合并操作,不过这很容易实现。有了这个简单的关系之后我们就完全可以用我们之前开发的代码,对这个连通性问题进行仿真。我们在足够大的N上运行足够多次的仿真获得结果 渗滤阈值大约是0.592746。
题解
https://www.jianshu.com/p/f2ba86a22b85
这里存储了问题很好的题解。但是他的第三种解答好像不对,hint中说到是按照第二题添加的find()的方法来做。
看这个简答比较好。https://boweixu.me/posts/intro-to-union-find-data-structure-exercise/
算法效率分析
介绍
例子:
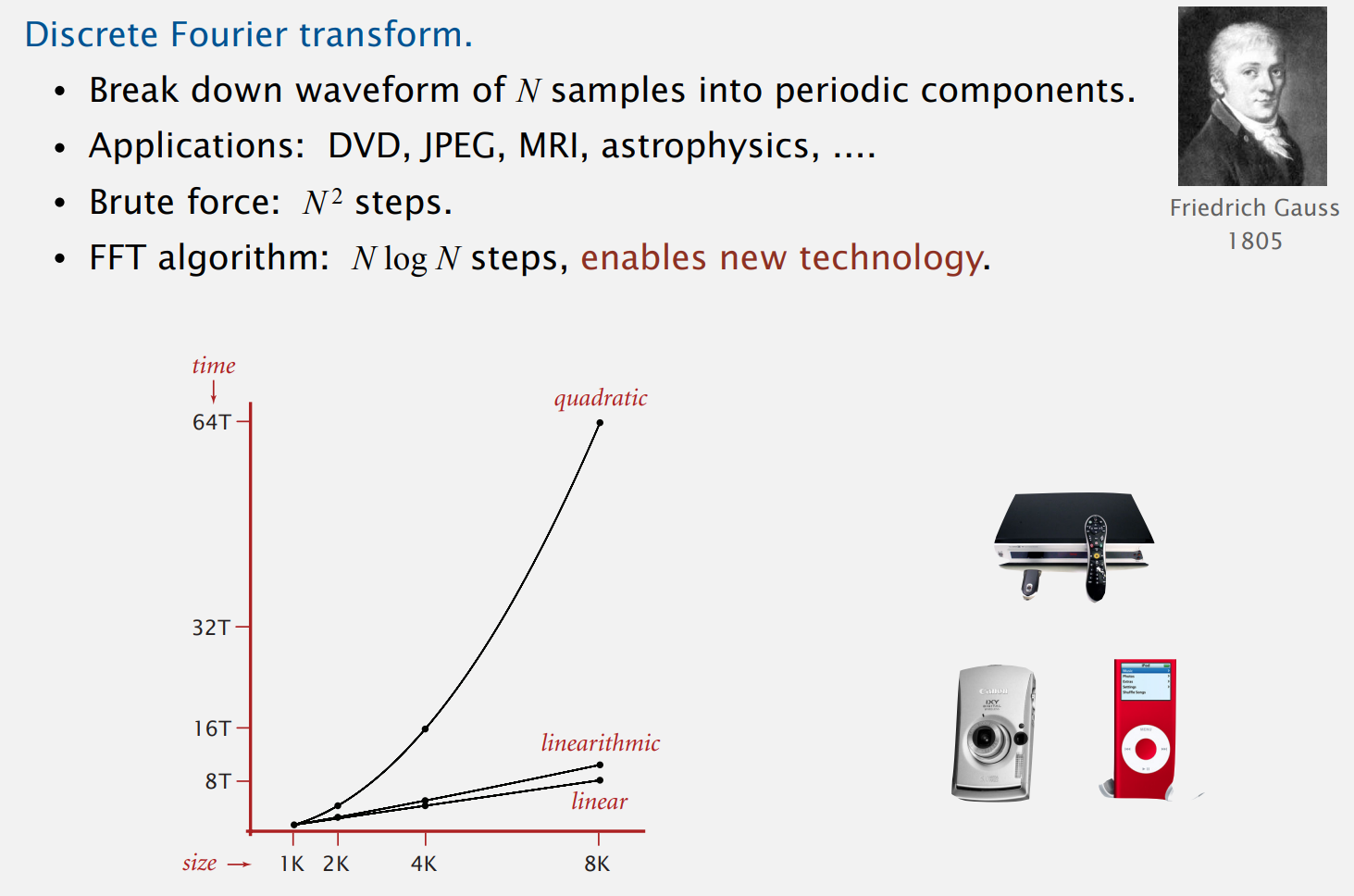
第一个也是最著名的就是FFT(快速傅立叶变换)算法,这个算法将信号的N个采样波形分为若干周期分量,这是DVD和JPEG以及很多其他应用的基础,有一个简单的方法需要正比于N^2的时间,但是FFT算法只需要NlogN 步。N logN和N^2的区别就是能否求解大型问题,这个快速算法使得我们今天很多数字媒体技术成为可能。
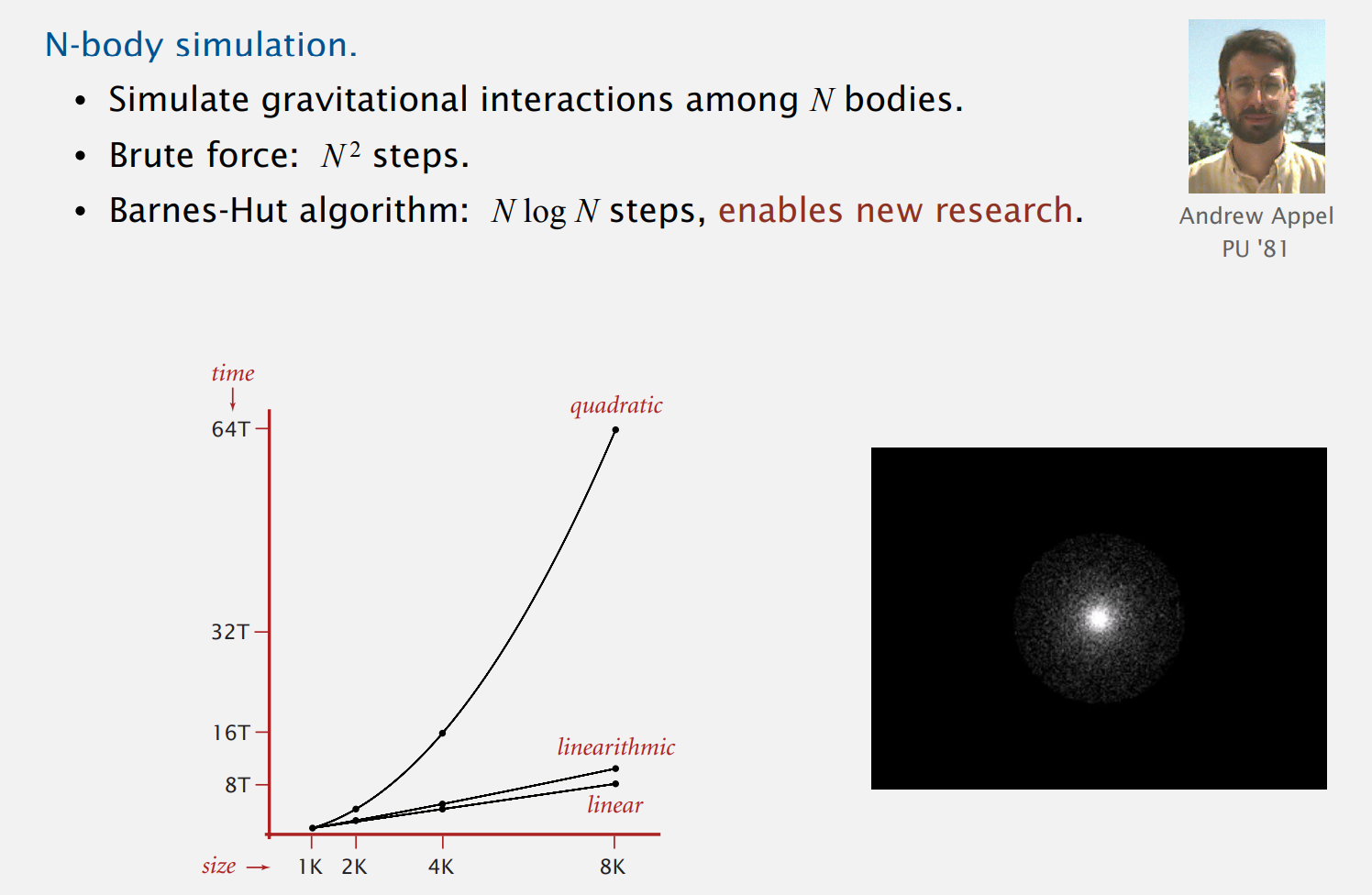
另一个例子实际上是Andrew Appel开发的,他现在是普林斯顿的计算机科学系主任。他还是本科生时做毕业论文的时候设计了这个算法,这个算法能够快速求解N体仿真问题,简单算法需要正比于N^2的时间,而Appel的算法是NlogN级别的算法。这意味着科学家能够运行巨大N值的N体仿真,这个算法催生了新的研究。
所以,我们常常面临的挑战是 我的程序能否求解实际中大型输入? 下图给出了科学方法与原则:

科学方法基本上是先观察,然后提出假设进行预测,比较预测结果与观察结果,再进行验证。使用科学方法,有一些基本原则。第一,如果要做实验,你应该期望别人做同样的实验也能有相同的结果。第二,假设必须具有某个特殊的性质,它能被实验证伪。所以提出假设必须小心谨慎。 即可复现性与可证伪性。
观察:以3-SUM为例
对于3-SUM问题(给N个数,问使和为0的三个数字的组合有多少个),可编写如下java程序求解:
其中,为了计算消耗的时间,这里用到了
Stopwatch.javaStopwatch.java 是一种测量程序运行时间的数据类型。:程序的总运行时间由两个主要因素决定:执行每条语句的成本和每条语句的执行频率。
Empirical analysis,假设运行结果如下表所示:
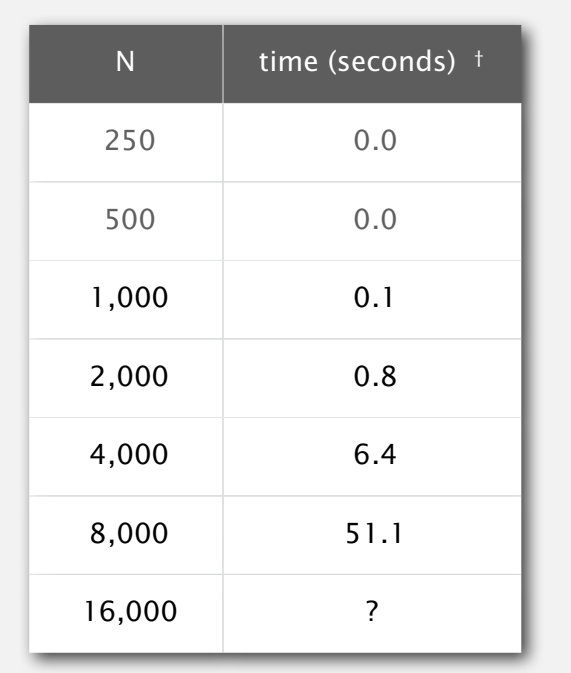
我们想要预测当N为16,000时,使用的时间。一个办法是使用双对数坐标绘图(log log plot),通常会得到一条直线,对于我们上述这个问题,绘制出来的图表是:
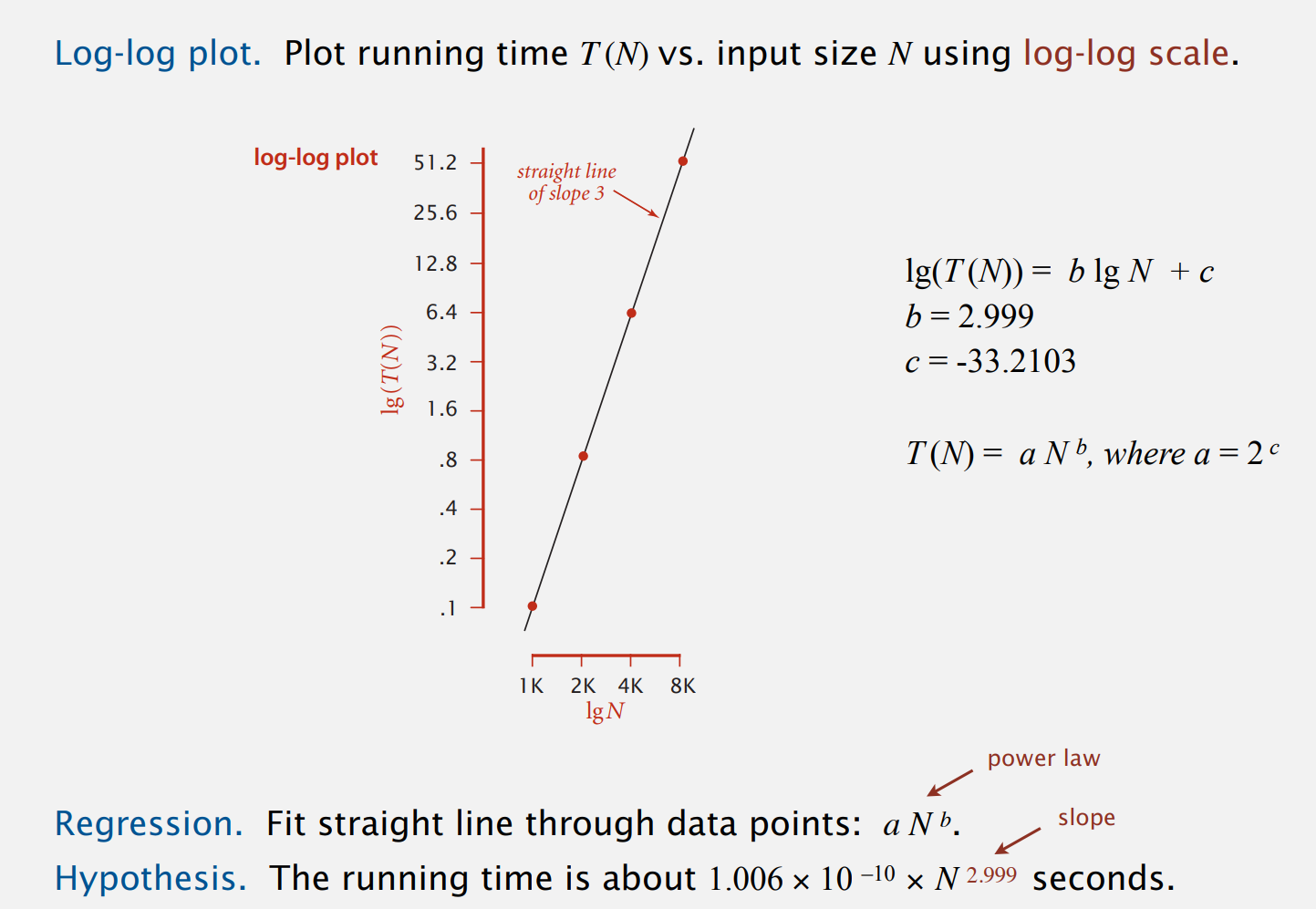
绘制出来的直线斜率为3,可以进行简单的数学推导:$$\lg(T(N)) = b\lg(N) + c \2 ^{\lg(T(N))} = 2^{(\lg(N)^b)}*2^c \T(N) = N^b * 2^c$$为了快速计算b,一种方法是每次将输入翻倍,然后计算出N和2N运行时间的比率,这个比率会收敛到一个常数。实际上比率的对数会收敛到N的指数,也就是我们要去求的b。推导很简单,$T(2N)/T(N) = 2^b$。

然后计算出b之后,我们找个最大的N的数据,带进去,就可以计算出a。
当然还有很多因素影响消耗的时间,系统性因素有硬件配置、软件环境等。
数学模型
下表给出了在特定的机器上一些基本数学运算所使用的时长,ns(nanosecond):纳秒,时间单位。 一秒的十亿分之一,等于10的负9次方秒(1 ns = 10 -9 s)。(毫秒,微秒,纳秒):
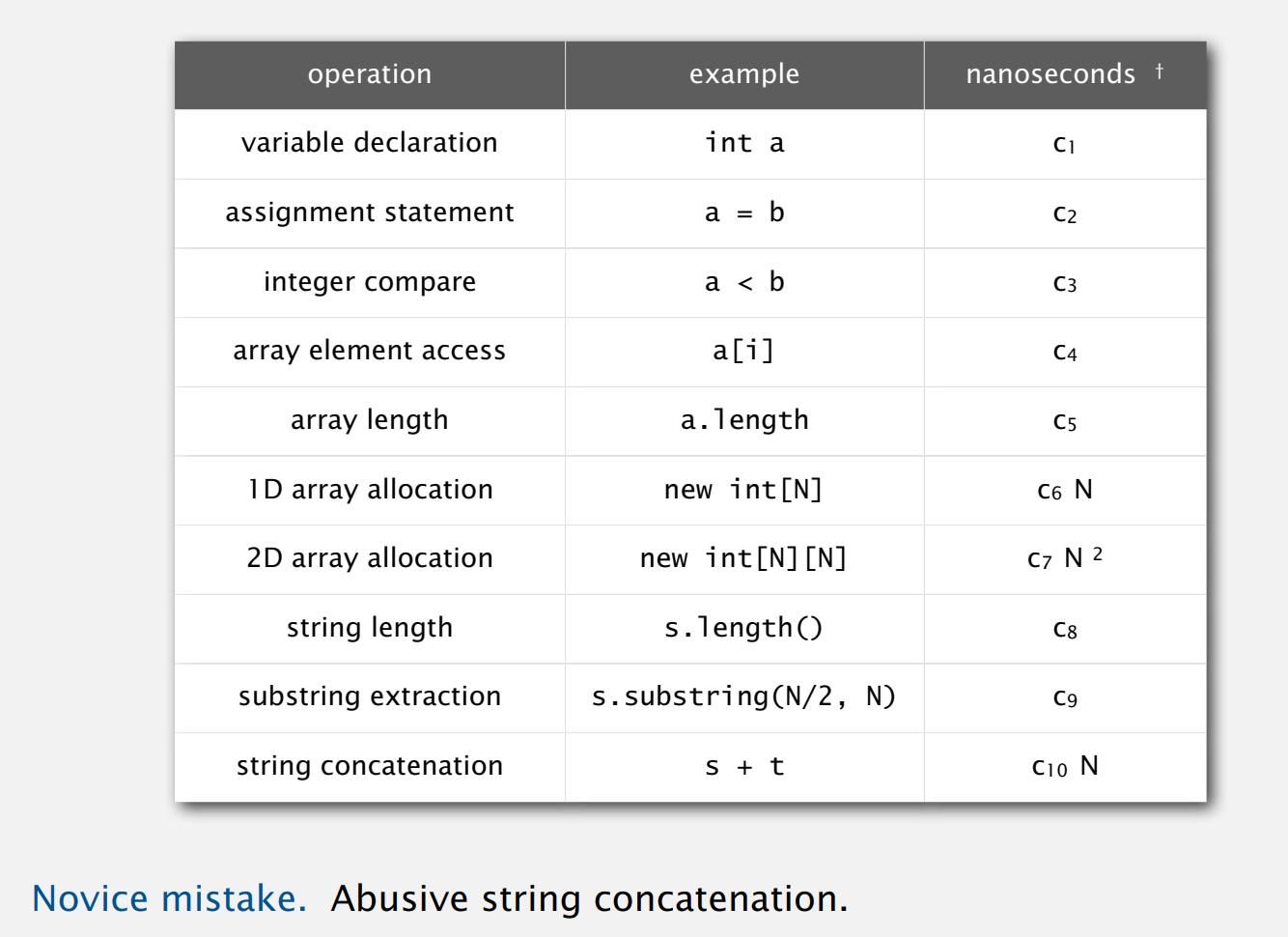
所以,我们办法有确定基本操作的开销。所以绝大多是情况下我们只要假定它是某个常数,而且你也能得知那个常数是多少。虽然当我们处理一组对象时,N个对象有一些操作需要的时间是和N成正比的,比如你要分配一个大小为N的数组,需要正比于N的时间,因为在Java中默认把数组中的每个元素初始化为0。其他操作取决于系统的实现。比如连接字符串是一个重要的操作如果连接两个字符串,运行时间与字符串的长度成正比。很多新手使用Java编程时错把连接字符串当作是常数时间的操作,而实际上并不是。
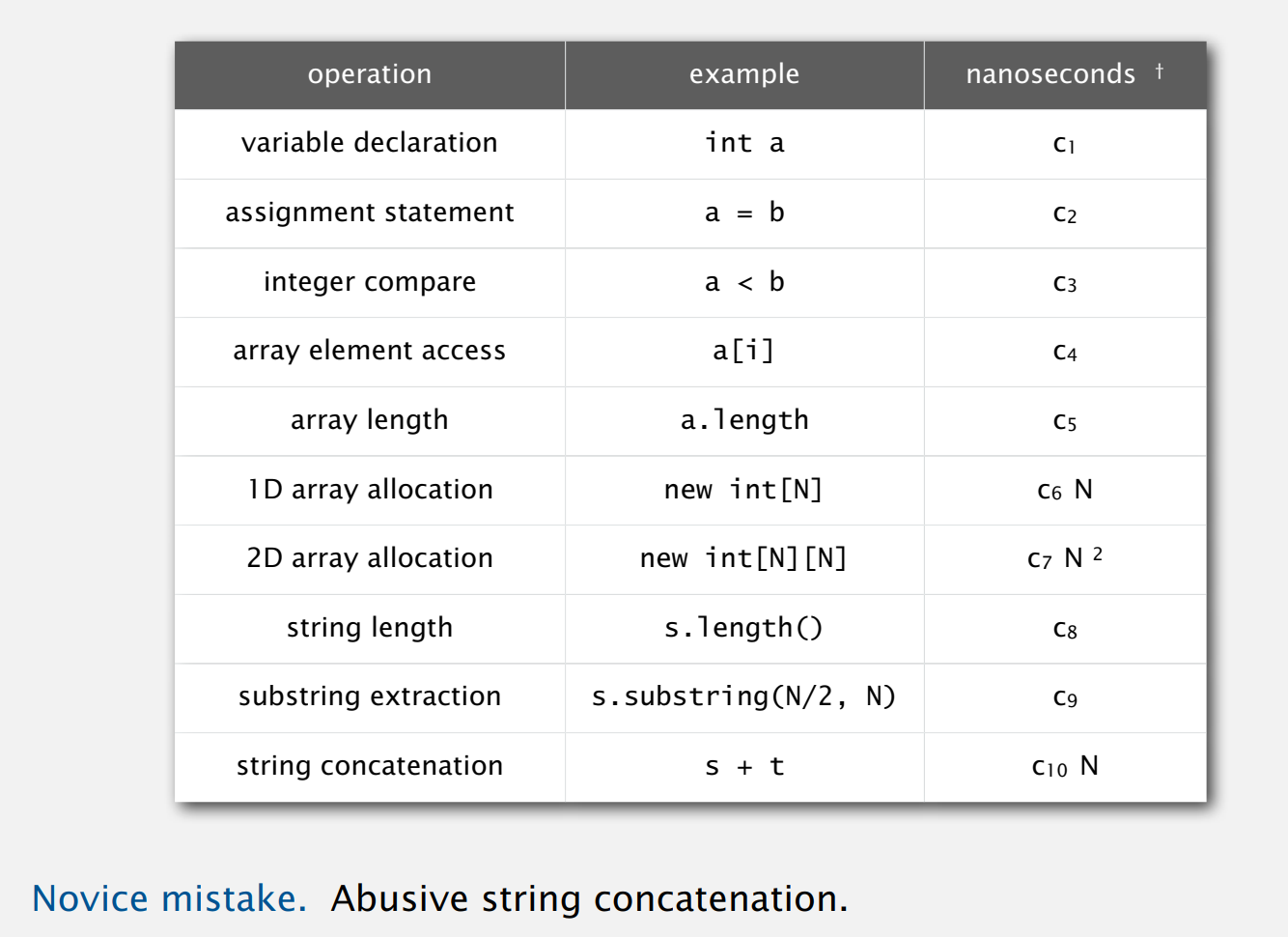
下图是一个2—SUM的例子:

可以看出这么做太繁琐了,接下来可以对其进行一些简化:

与其钻到程序里,然后统计每个小细节,我们选出开销最大的基本操作或者执行次数最多的,用开销最大频率最高的操作来代表执行时间。一般,我们假设实际的运行时间就是常数乘以这个操作的执行时间。在上面这个例子中,我们选择访问数组的时间作为代表。

第二个简化是忽略推导出的式子中的低阶项。用这种波浪号可以很容易实现。这种简化的思想就是当式子中的N很大时,N^3比N这一项或者16要大得多。实际上,大到几乎注意不到低阶项。所以这些式子近似为1/6 N^3,这是对这些量很好的近似。所以丢掉这些低阶项极大地简化了计算。波浪号的具体严格定义:g(N) ~ f(N) 表示随着 N 的增长,g(N) / f(N) 趋近于 1。
所以对于3-SUM问题,计算出来的近似为(3个循环所以要乘以3):

一些数学运算:

下面是一道简单的测试题:

答案为$\frac{3}{2}n^2\lg n$:

增长顺序的分类:以二分查找为例
好消息是,基本上只有这几种增长分类(下绘制双对数图):
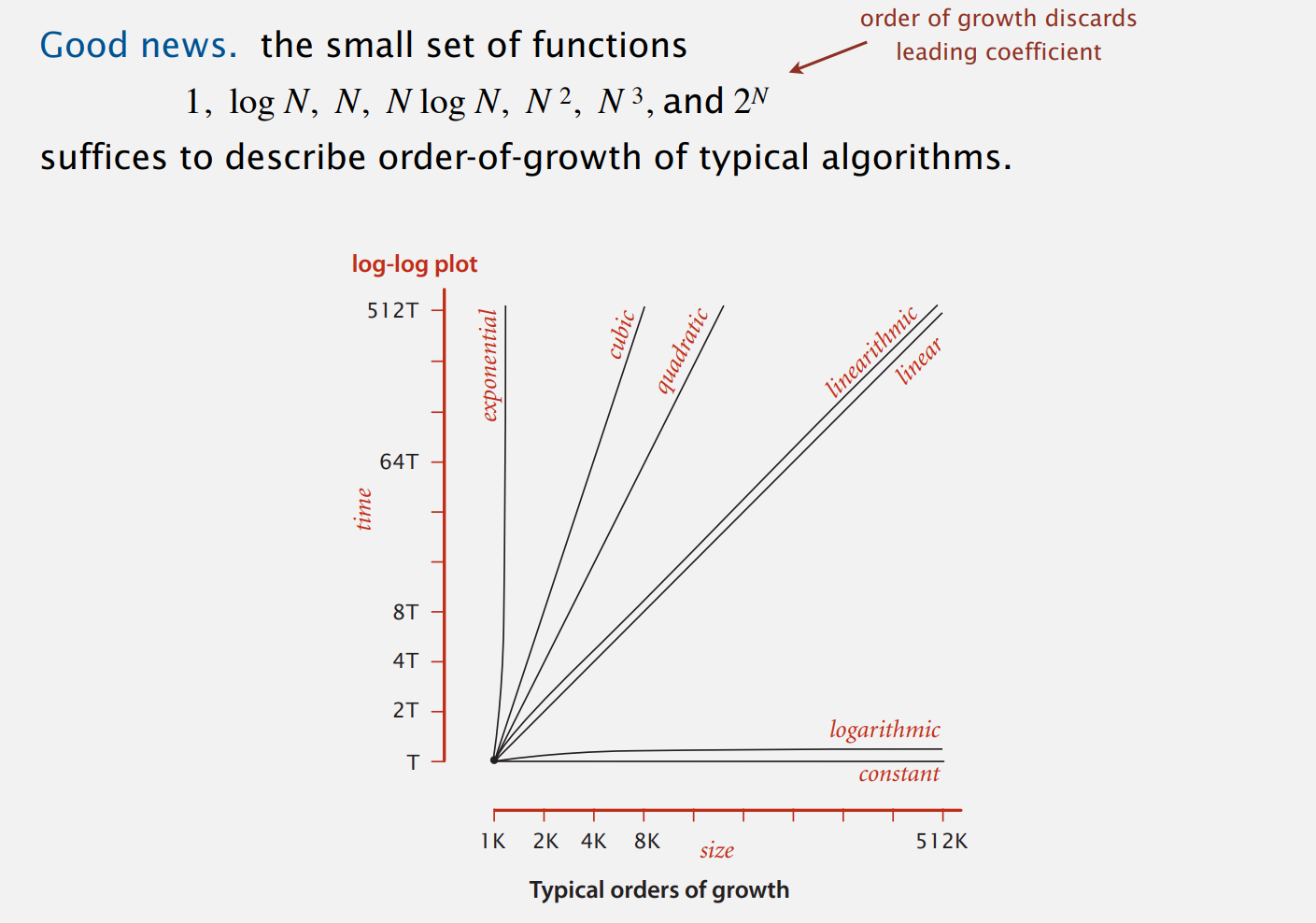
一些简单的模式:
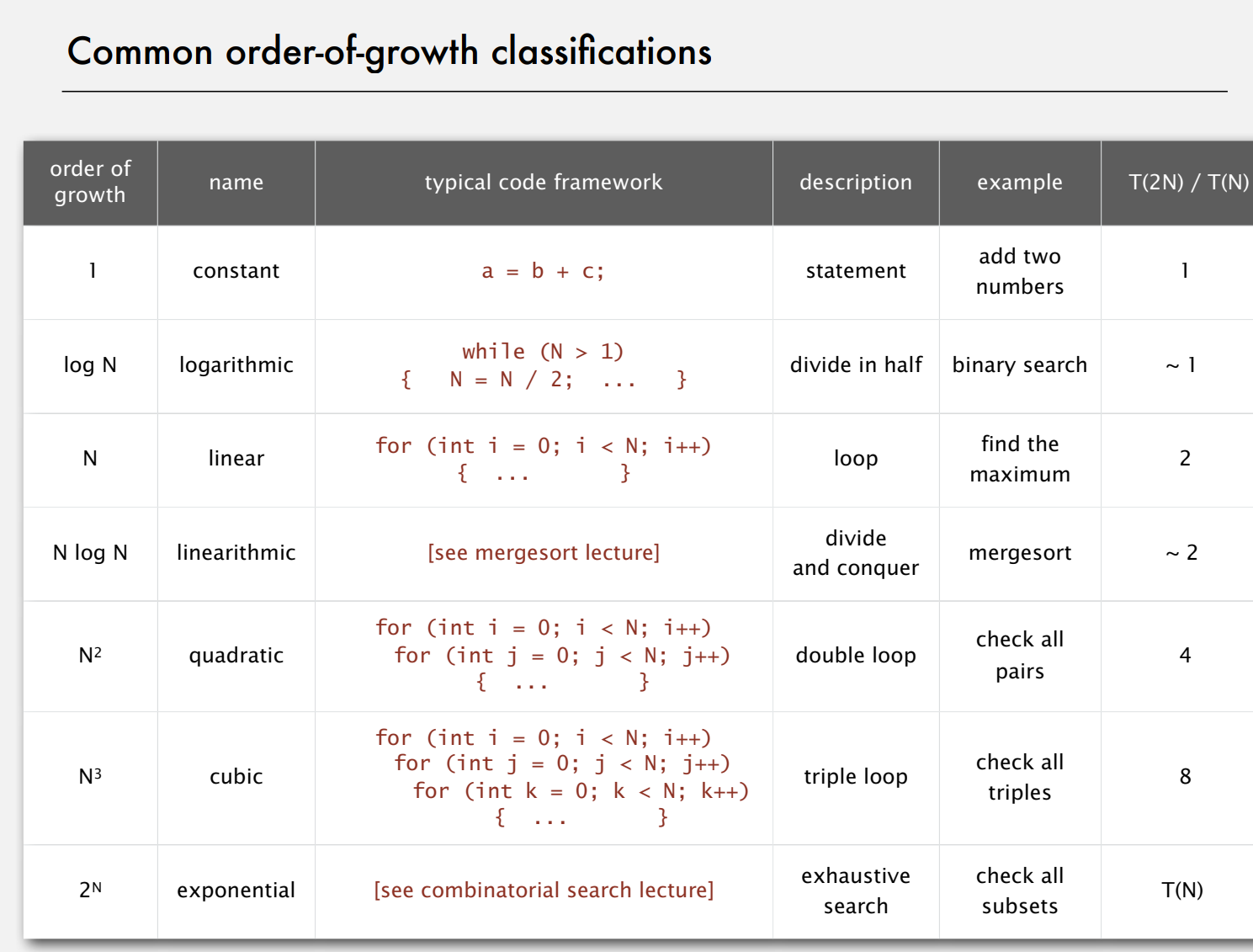
下面是二分查找代码的链接:
https://algs4.cs.princeton.edu/code/edu/princeton/cs/algs4/BinarySearch.java.html
数学推理证明二分查找最多进行$1+\lg N$次比较。
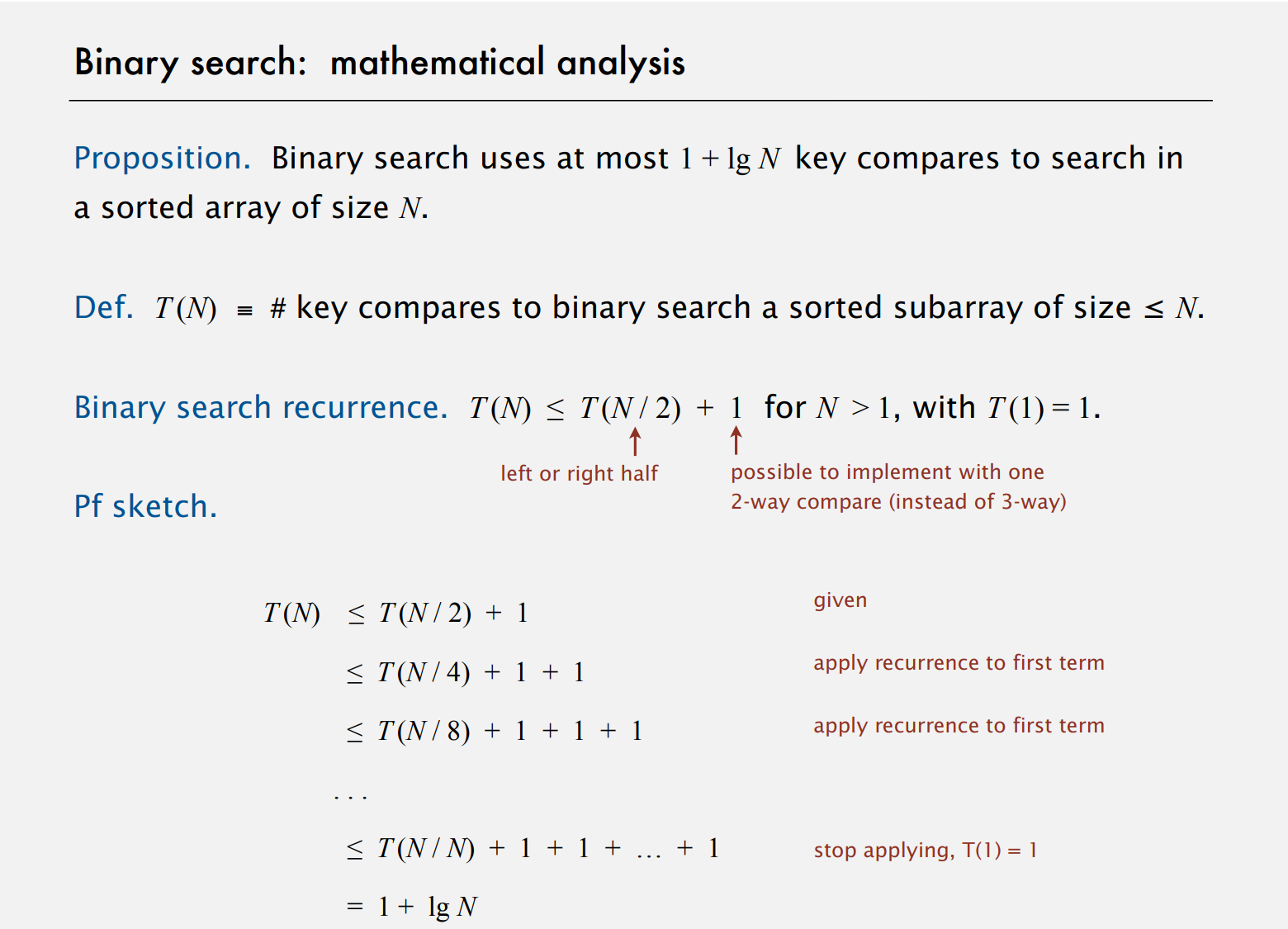
这里只证明了N是2的幂的情况,不是这样的情况也可以给出同样的证明。
因此,使用二分查找,就可以改进3-SUM问题。

首先,对N个数进行排序,插入排序增长顺序是$N^2$,然后取i,j为一对,始终保持i<j<k,算出已知ij的时候使得和为0的那个k,然后在大于j的数中二分搜索k,增长顺序为$N^2 \log N$。这样子改进后的3—SUM算法会比原先的$N^3$快上许多。改进后的快速3-SUM算法的链接:
https://algs4.cs.princeton.edu/code/edu/princeton/cs/algs4/ThreeSumFast.java.html
算法理论
一些记号,大Theta,大O与大Omega:
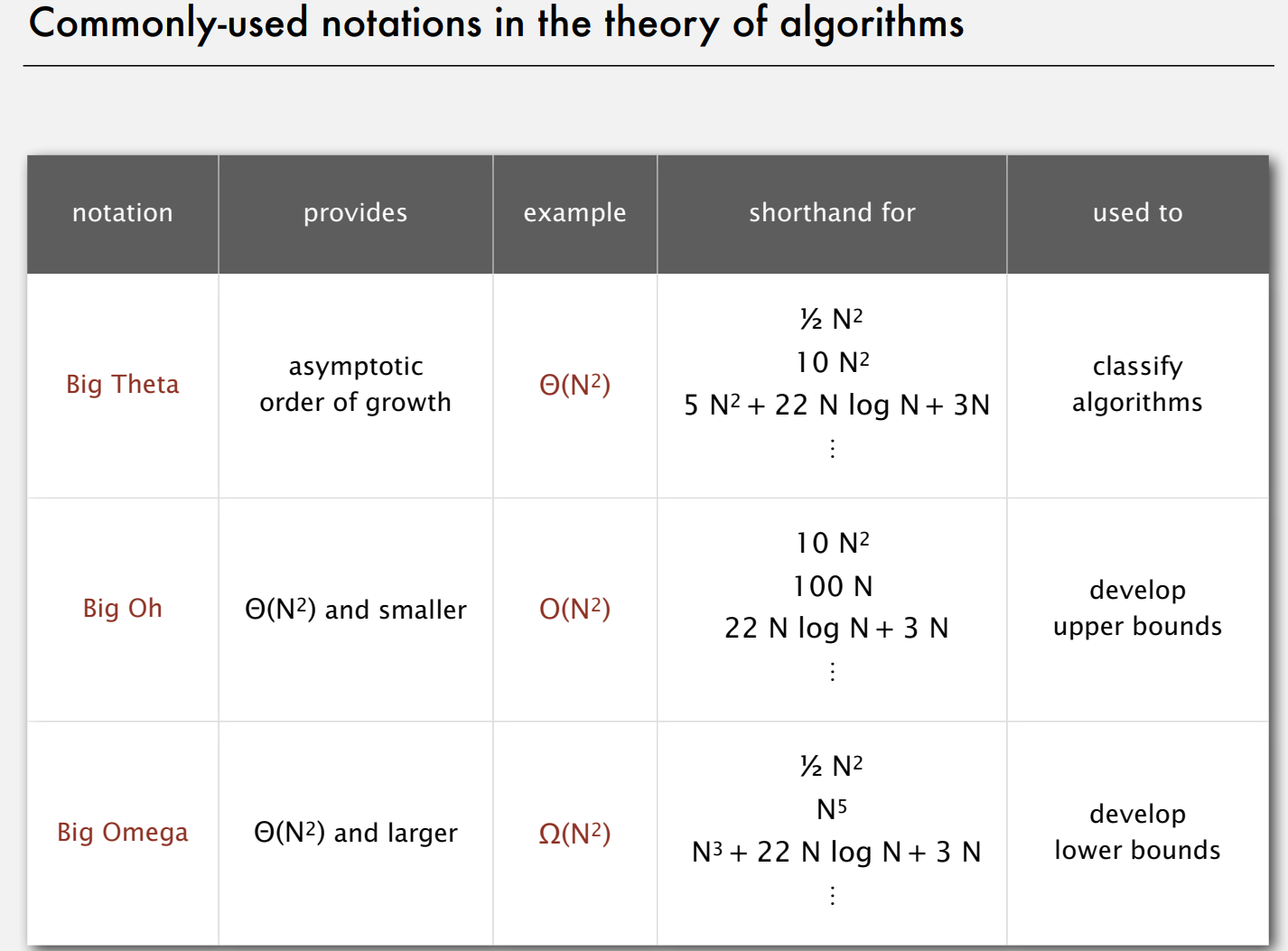
我们以3-SUM问题为例进行分析:

对于改进后的fast 3—SUM,我们可以知道算法运行的上界是$O(N^2\log N)$,算法运行的下界,由于我们需要至少遍历所有的数值,所以是$\Omega(N)$。
很多人错把O分析的结果当作了运行时间的近似模型,其实应该是问题更好的上界,这是个大错误。这门课中,我们使用波浪记号来表示近似模型。对于某些我们感兴趣特定的量会给出特定的结果,运行时间中非特异的常数和机器与系统的性质相关,使用这样的结果我们就能预测并比较算法的性能。
例题:

Recall that big-Oh notation provides only an upper bound on the growth rate of a function as n gets large. In this course, we primarily use tilde notation because it more accurately describes the function—it provides both an upper and lower bound on the function as well as the coefficient of the leading term.
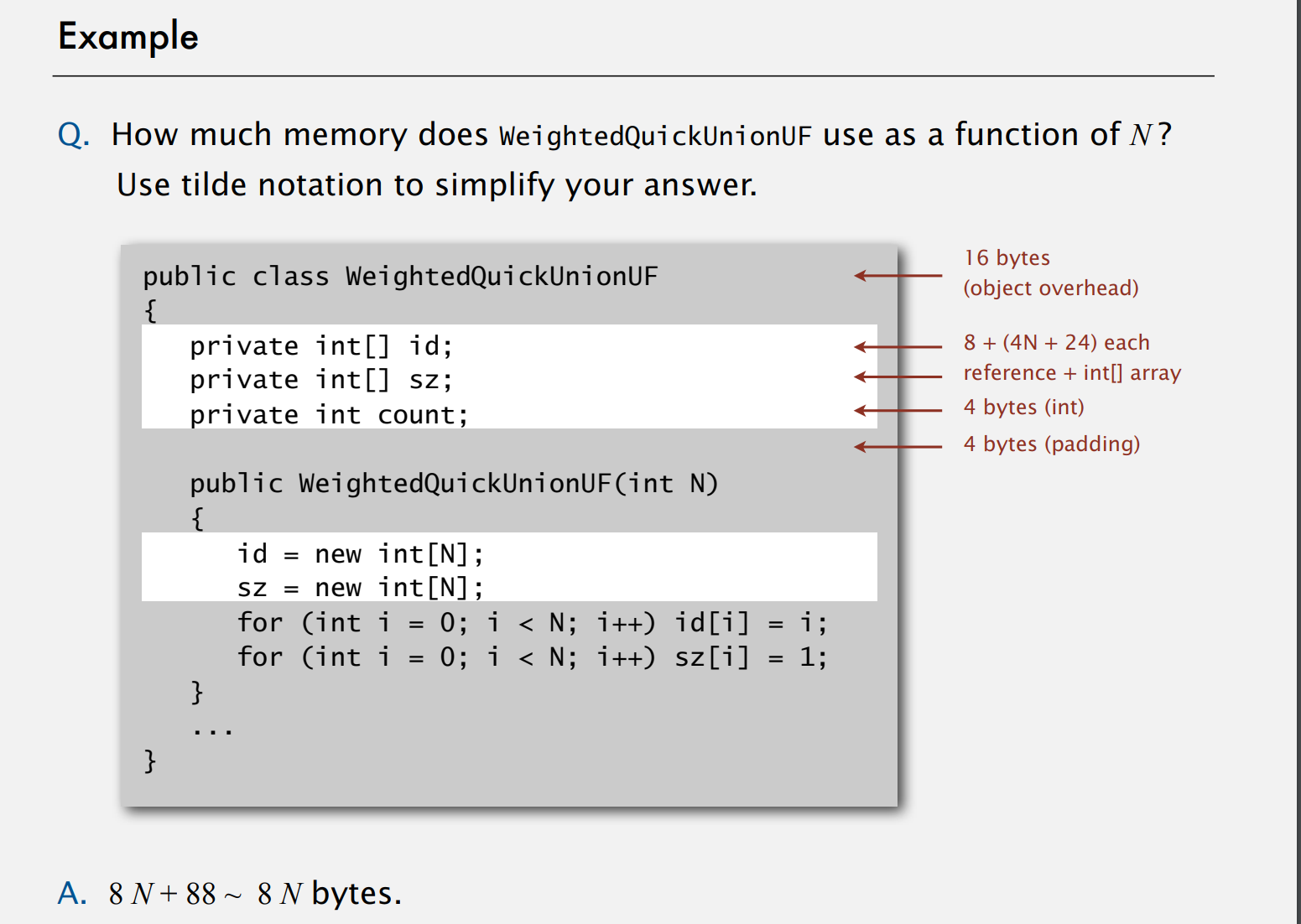
内存需求

对于MB的定义其实还是有争议的,大部分计算机科学家将其定义为$2^{20}$字节。现在的计算机多是64位操作系统,这允许我们储存更多地址,但是指针却用了更多的空间。
下面是一些典型的原始数据类型和数组的内存消耗:

大多数应用中,我们使用双精度浮点型表示浮点数,普通整型表示整数,这些是原始类型。对于数组来说 每个数组都有固定的保留数量,如果它有N个项目,它会增加N个项目的原始类型的成本,一个双精度浮点型数组会占用8N+24个字节。还有二维数组,对于二维的双精度数组, 大约为8MN,尽管头部会造成额外的开销,对于一个足够大的MN数组来说 这已经很准确了,这是在典型的实现中原始类型和数组的使用方法。
由于还需要进行padding(填充),在下面的例子中,padding也需要4字节,对象开销为16个字节,所以一共是32字节。

另一个例子:

然后这里是典型的一些数据结构所使用的内存:

例题:
题解
- 3-SUM in quadratic time. Design an algorithm for the 3-SUM problem that takes time proportional to n^2 in the worst case. You may assume that you can sort the n integers in time proportional to n^2 or better. 二次时间的 3-SUM。 为 3-SUM 问题设计一个算法,在最坏的情况下,该算法所花费的时间与 n^2 成正比。您可能会假设您可以按与 n^2 或更好的时间比例对 n 个整数进行排序。
Here's one approach to solve the 3-SUM problem in time proportional to n^2:
- Sort the input array of n integers in time proportional to n^2 or better.
- For each integer i in the array, use two pointers (left and right) to find all pairs of integers that sum up to the target value -i.
- To avoid duplicates, make sure that the left pointer and right pointer don't point to the same element. Also, make sure that when the left pointer moves to the right, it never goes back to the same position it was in previously.
- Return true if any such pair is found, otherwise return false.
The time complexity of this algorithm is O(n^2), as each iteration of the outer loop takes O(n) time and is executed n times, making the total time complexity O(n^2).这是及时解决与 n^2 成比例的 3-SUM 问题的一种方法:按与 n^2 或更好的时间比例对 n 个整数的输入数组进行排序。对于数组中的每个整数 i,使用两个指针(左指针和右指针)找到总和为目标值 -i 的所有整数对。为避免重复,请确保左指针和右指针不指向同一元素。另外,确保当左指针向右移动时,它永远不会回到之前的相同位置。如果找到任何这样的对,则返回 true,否则返回 false。该算法的时间复杂度为 O(n^2),因为外循环的每次迭代都需要 O(n) 时间并执行 n 次,使得总时间复杂度为 O(n^2)

- Search in a bitonic array. An array is bitonic if it is comprised of an increasing sequence of integers followed immediately by a decreasing sequence of integers. Write a program that, given a bitonic array of n distinct integer values, determines whether a given integer is in the array.
- Standard version: Use ~3lgn compares in the worst case.
- Signing bonus: Use ∼2lgn compares in the worst case (and prove that no algorithm can guarantee to perform fewer than ∼2lgn compares in the worst case). 在双调数组中搜索。如果一个数组由递增的整数序列组成,紧接着是递减的整数序列,则该数组是双调的。编写一个程序,给定一个包含 n 个不同整数值的双调数组,确定给定整数是否在数组中。- 标准版:在最坏情况下使用 ~3lgn 进行比较。- 签名奖励:在最坏情况下使用~2lgn 比较(并证明没有算法可以保证在最坏情况下执行少于~2lgn 比较)。
Here's one approach to solve the standard version of the problem, using ~3lgn compares in the worst case:
- Use binary search to find the maximum element in the bitonic array in O(logn) time.
- Divide the bitonic array into two parts: the increasing sequence (left of the maximum element) and the decreasing sequence (right of the maximum element).
- Use binary search to search for the target element in the increasing sequence, if it is found return true.
- Use binary search to search for the target element in the decreasing sequence, if it is found return true.
- If the target element is not found in either the increasing or decreasing sequence, return false.
This approach uses a total of 3 log n compares in the worst case (1 for finding the maximum element and 2 for searching in the increasing and decreasing sequences).For the signing bonus version of the problem, it can be shown that no algorithm can guarantee to perform fewer than 2lgn compares in the worst case. This is because the worst case occurs when the target element is not in the array, and in this case, we have to search both the increasing and decreasing sequences to determine that it is not there. Since each binary search takes logn time, the total time complexity is 2logn.这是解决问题标准版本的一种方法,在最坏的情况下使用 ~3lg n进行比较:使用二进制搜索在 O(logn) 时间内找到双调数组中的最大元素。将双调数组分为两部分:递增序列(最大元素左侧)和递减序列(最大元素右侧)。使用二分查找从递增的序列中查找目标元素,如果找到则返回true。使用二分查找,按降序查找目标元素,找到则返回true。如果在递增或递减序列中均未找到目标元素,则返回 false。这种方法在最坏情况下总共使用 3 log n 比较(1 次用于查找最大元素,2 次用于在递增和递减序列中搜索)。对于问题的签名奖金版本,可以证明没有算法可以保证在最坏情况下执行少于 2lg n次比较。这是因为最坏的情况发生在目标元素不在数组中时,在这种情况下,我们必须同时搜索递增和递减序列以确定它不存在。由于每次二分查找需要 logn 时间,所以总时间复杂度为 2logn

- Egg drop. Suppose that you have an n-story building (with floors 1 through n) and plenty of eggs. An egg breaks if it is dropped from floor T or higher and does not break otherwise. Your goal is to devise a strategy to determine the value of T given the following limitations on the number of eggs and tosses:
- Version 0: 1 egg, ≤T tosses.
- Version 1: ∼1lgn eggs and ∼1lgn tosses.
- Version 2: ∼lgT eggs and ∼2lgT tosses.
- Version 3: 2 eggs and ∼2n tosses.
- Version 4: 2 eggs and $c \sqrt T$ tosses for some fixed constant c. 鸡蛋掉落。 假设您有一栋 n 层楼的建筑(从 1 层到 n 层)和大量鸡蛋。如果鸡蛋从地板 T 或更高处掉落,它就会破裂,否则不会破裂。你的目标是设计一个策略来确定 T 的值,给定以下鸡蛋和抛掷次数的限制: - 版本 0:1 个鸡蛋,≤T 抛掷。- 版本 1:~1lgn 个鸡蛋和~1lgn 个抛掷。- 版本 2:∼lgT 鸡蛋和∼2lgT 抛掷。- 版本 3:2 个鸡蛋和 ∼2n 次抛掷。- 版本 4:2 个鸡蛋和 $c \sqrt T$ 投掷以获得某个固定常数 c。
Here's one approach to solve each version of the egg drop problem:
- Version 0: With only 1 egg and T tosses, a straightforward strategy is to start from floor 1 and increment the floor after each toss, until the egg breaks. The value of T can be found in at most T tries, but this approach is not optimal as it takes the maximum number of tries in the worst case scenario.
- Version 1: With approximately log n eggs and approximately log n tosses, the egg drop problem can be solved by dividing the n-story building into log n intervals, and throwing an egg from the top of each interval. If an egg breaks on the kth interval, then T is in the k-1 intervals below it. Repeat the process, reducing the number of intervals by half after each try, until T is found. This approach will find T in at most log n tries.
这是解决每个版本的鸡蛋掉落问题的一种方法:版本 0:只有 1 个鸡蛋和 T 次抛掷,一个简单的策略是从第 1 层开始,每次抛掷后增加楼层,直到鸡蛋打破。T 的值可以在最多 T 次尝试中找到,但这种方法不是最优的,因为它在最坏的情况下进行了最大次数的尝试。版本 1:大约 log n 个鸡蛋和大约 log n 次抛蛋,可以通过将 n 层建筑物分成 log n 个区间,并从每个区间的顶部扔一个鸡蛋来解决鸡蛋掉落问题。如果一个鸡蛋在第 k 个区间破了,那么 T 在它下面的 k-1 个区间内。重复该过程,每次尝试后将间隔数减半,直到找到 T。这种方法将在最多 log n 次尝试中找到 T。这里chatgpt给出的答案不对。

这个网址有好的解决方案。
https://truongtx.me/2018/05/06/solutions-to-egg-drop-problem
- 作者:很久不是自己
- 链接:https://weibo.com/article/algs-1
- 声明:本文采用 CC BY-NC-SA 4.0 许可协议,转载请注明出处。
相关文章